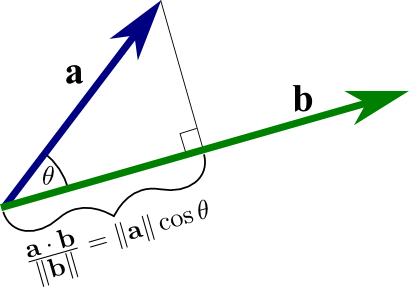
In mathematics, a product can be defined as the resultant value of two numbers when multiplied. The dot product can be defined as the way of multiplying more than two vectors. You may notice the unique fact about dot products that the resultant value of a dot product is always a scalar quantity. The quantity that is only derived with the help of magnitude can be defined as the scalar quantity. Some examples of it are as follows: density, speed, time, mass, and so on. Another way of multiplying vector areas is by the use of a cross-product formula. In this article, we will try to cover some interesting topics related to dot products and do a brief analysis about them.
What Are Vectors?
An entity that consists of both magnitude and direction is known as the vector. A vector is expressed or represented through the help of arrows that have the starting/initial point and ending/terminal points. If we go along the lines of history we may find that the term vector was first used around 200 years ago which is about the 1820s. The use of it can be seen in both the world of mathematics and physics. Like every other term, vectors also possess some properties which are very important in order to solve questions about them. Some examples of the vectors are as follows: displacement, force, acceleration, velocity, and so on which consist of magnitude and directions are the examples of vectors.
Various Different Types of Vectors
As mentioned above, a geometrical entity that includes both the magnitude and direction can be defined as vectors. There are various types of vectors having different properties and nature. The following points analyze the types of vectors in a detailed manner.
- A vector that has the value of zero for the magnitude can be defined as the zero vector. The zero vector is also known as the additive identity/property of the vectors.
- A vector that has the value of one for the magnitude can be defined as the unit vector. The unit vector is also known as the multiplicative identity/property of the vectors.
- A vector that is used to calculate the direction of the movement of a vector and its position can be defined as the position vector. The position vector is also defined as the location vector.
- Whenever the value of the magnitude is equal in two vectors, those vectors are said to be equal vectors. Along with the magnitude, the direction is also the same for the equal vectors.
- Whenever the direction of two vectors is opposite to each other, they are said to be negative vectors. Similarly, when the direction of movements of two vectors is the same, they are said to be parallel vectors.
- If the angle of degree between two vectors is equivalent to 90 degrees, it is said to be an orthogonal vector. A type of vector which has the same initial or starting point is said to be defined as the co-initial vector.
If you want to learn about dot products in a detailed, fun, and in interactive manner visit Cuemath.
Learn Math from Online Math Classes
Cuemath is an online platform that deals with the study of mathematics online. Mathematics as a subject requires conceptual clarity in order to reach good heights and excel in the given topic. The online math classesprovide you with highly qualified teachers with good experience, curated live sessions, doubt clearing classes, and many more. It also helps you to study math in a fun way as it provides you with math puzzles and math worksheets. In order to enroll in online math classes visit Cuemath.